목적
오늘은 SAS 프로그램을 이용하여 세 집단 이상의 평균을 비교하는 방법에 대해 알아보자.
SAS를 이용하여 분석할 것이고, Sample data는 sashelp.cars를 이용할 것이다. 예시 자료를 이용하여 Asia, Europe, USA의 차량 엔진 크기가 차이가 있는지를 보고자 한다.
1. 정규성 검정
- 집단이 정규성을 띄는가를 확인할 수 있다.
- 모든 집단이 정규성을 만족하면 모수적 방법인 One-way ANOVA 를 이용, 아니라면 이의 비모수적 방법인 Kruskal-Wallis test 를 이용하여 분석한다.
| proc univariate data=sashelp.cars normal; class Origin; var EngineSize; run; |
<Origin=Asia> <Origin=Europe>  <Origin=USA>  |
정규성 검정도 여러가지 방법이 있지만 Shapiro-Wilk 결과를 보는 것이 일반적이다.
세 집단의 정규성 검정 결과 p 값이 모두 유의수준 0.05 미만이므로 자료는 정규성을 띄지 않는다고 볼 수 있다.
비모수적 검정 방법인 Kruskal-Wallis test 를 시행한다.
2. Kruskal-Wallis test
세 집단 이상의 중위수를 비교하는 방법
귀무가설 (H0) 은 m1=m2=m3=...=mN, 대립가설 (H1) 은 Not H0 (적어도 한 집단은 다르다.)
| proc npar1way data=sashelp.cars wilcoxon; class Origin; var EngineSize; run; |
 |
p값은 <.0001 로 α=0.05 하에서 지역 간 엔진 크기의 중위수는 차이가 있다는 결론을 얻을 수 있다.
3. One-way Analysis of Variance (ANOVA)
- 세 집단 이상의 평균을 비교하는 방법
- 귀무가설 (H0) 은 μ1=μ2=μ3=...=μN, 대립가설 (H1) 은 Not H0 (적어도 한 집단은 다르다.)
- 기본 가정: 집단들은 서로 독립 (독립성 가정), 정규성 가정, 등분산성 가정
| proc anova data=sashelp.cars; class Origin; model EngineSize= Origin; run;quit; |
  |
p값은 <.0001 로 α=0.05 하에서 지역 간 엔진 크기의 평균은 차이가 있다는 결론을 얻을 수 있다.
4. 사후검정
ANOVA 결과 지역 간 엔진 크기의 평균은 차이가 있다는 결론을 얻었는데, 그럼 어떤 집단이 차이가 있는 것인가? 사후 검정을 해보자. 다만 본 포스팅에는 다중 검정으로 인한 1종 오류 보정 방법에 대한 내용은 다루지 않기로 한다.
| proc anova data=sashelp.cars; class Origin; model EngineSize= Origin; means Origin / lsd; run;quit; |
 |
*** 표시된 항목은 유의하다는 것인데, 모든 경우에 지역간 엔진 크기의 평균은 차이가 있다는 결론을 얻을 수 있다.
5. 등분산성 검정
사실 위 ANOVA 검정을 보기 전에 등분산성 검정을 먼저 해야하는데,,
| proc anova data=sashelp.cars; class Origin; model EngineSize= Origin; means Origin / lsd hovtest welch; run;quit; |
<등분산성 검정> <Welch의 ANOVA 검정> 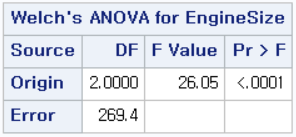 |
본 예제는 등분산성 검정의 p값은 0.0062 로 α=0.05 하에서 귀무가설을 기각하여 집단 간 분산들이 다르다는 것을 알 수 있고, 집단 간 분산이 다른 경우에는 Welch의 ANOVA 검정을 이용한다.
위와 동일하게 p값은 <.0001로 α=0.05 하에서 지역 간 엔진 크기의 평균은 차이가 있다는 결론을 얻을 수 있다.
'끄적이는 통계분석 > SAS를 이용한 통계분석' 카테고리의 다른 글
| SAS를 이용한 짝지은 비율에 대한 비교 (Mcnemar's test, Bowker's test) (0) | 2022.08.25 |
|---|---|
| SAS를 이용한 카이제곱 적합도 검정 (One way Chi-square test) (0) | 2022.08.24 |
| SAS를 이용한 비율에 대한 비교 (Chi-square test, Fisher's exact test) (0) | 2022.08.18 |
| SAS를 이용한 대응비교 검정(Paired t-test, Wilcoxon's sign rank test) (3) | 2019.01.19 |
| SAS를 이용한 두 집단의 평균 비교 (Independent t-test, Wilcoxon's rank sum test) (0) | 2019.01.17 |